
内功修炼 - 排序算法(上) 冒泡、插入、选择排序算法
前言
算法就是程序员的内功。这里介绍最常用的几大排序算法,排序分为内部排序和外部排序。
- 若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
- 若参加排序的记录数量很大,排序过程不可能在内存中完成,则称为外部排序。
排序方法分类
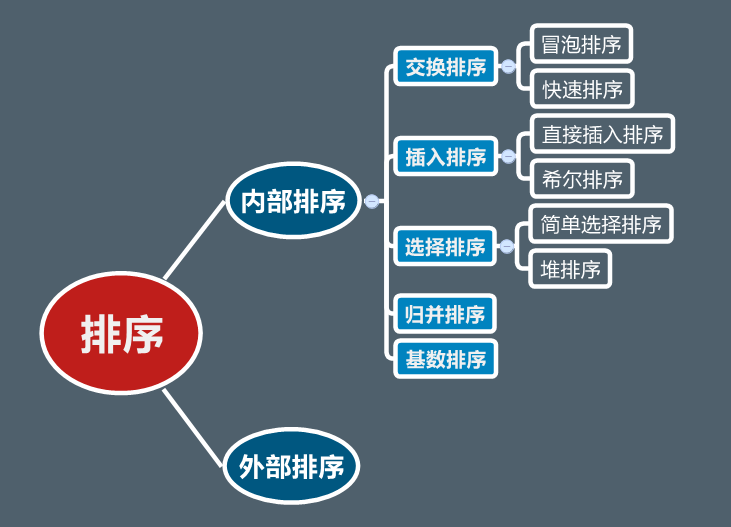
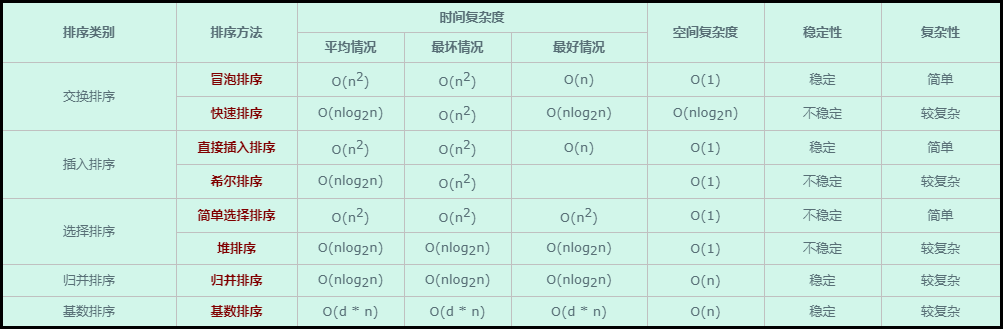
常见排序方法性能对比
冒泡排序 - O(n^2 )
简介
| 说明 | 描述 |
|---|---|
| 算法名 | Bubble Sort |
| 难度系数 | ★ |
| 算法复杂度 | O(n^2 ) |
| 缺点 | 如果是本身是倒序的,则会出现最坏的情况 O(N^2 ) |
性能
当数据越接近正序时,冒泡排序性能越好。
图解
趟数从0开始算每一趟,列表相邻两前面比后面大则交换位置, 每一趟无序的少一个,有序的多一个数, 如果一趟没有一个交换位置,那么这一趟之后就完成了。
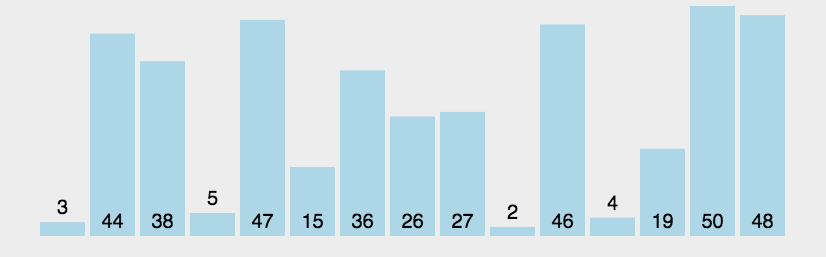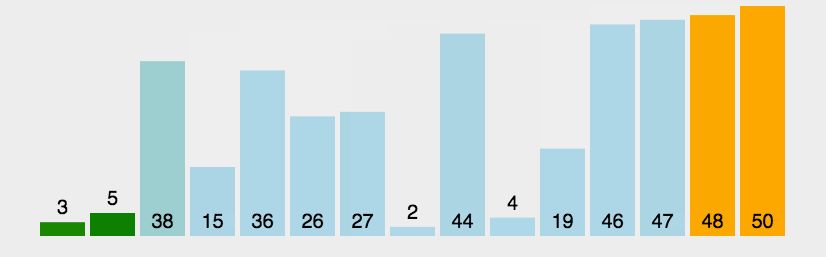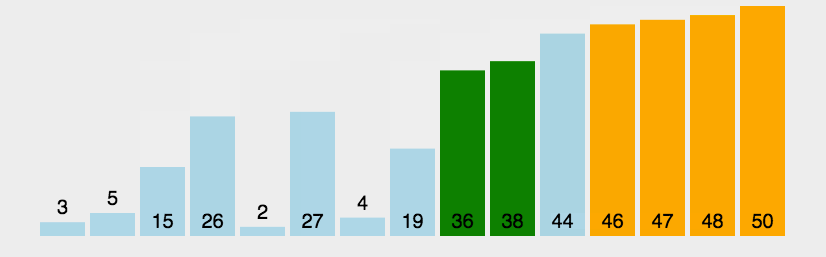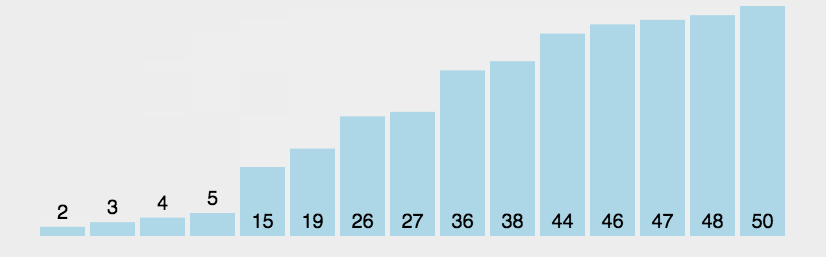
假设有一个大小为 N 的无序序列。以升序冒泡排序为例,冒泡排序就是要每趟排序过程中通过两两比较相邻元素,将小的数字放到前面,大的数字放在后面。
代码实现
1 | def bubble_sort(li): |
运行结果
选择排序 - O(n^2 )
简介
| 说明 | 描述 |
|---|---|
| 算法名 | Select Sort |
| 难度系数 | ★ |
| 算法复杂度 | O(n^2 ) |
| 缺点 | 多生成了一个列表多占了内存空间! |
性能

简单选择排序的比较次数与序列的初始排序无关。 假设待排序的序列有 N 个元素,则比较次数总是N (N - 1) / 2。
- 而移动次数与序列的初始排序有关。当序列正序时,移动次数最少,为 0.
- 当序列反序时,移动次数最多,为3N (N - 1) / 2。
所以,综合以上,简单排序的时间复杂度为 O(N^2 )。
图解
- 从待排序序列中,找到关键字最小的元素;
- 如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
- 从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。

如图所示,每趟排序中,将当前第 i 小的元素放在位置 i 上。

代码实现
1 | def select_sort(li): |
插入排序 - O(n^2 )
简介
| 说明 | 描述 |
|---|---|
| 算法名 | Insert Sort |
| 难度系数 | ★ |
| 算法复杂度 | O(n^2 ) |
| 缺点 | 最坏情况倒序 |
性能
类似玩扑克,每次从无序区摸一张,插到手里的有序区
- 当数据正序时,执行效率最好,每次插入都不用移动前面的元素,时间复杂度为O(N)。
- 当数据反序时,执行效率最差,每次插入都要前面的元素后移,时间复杂度为O(N^2 )。
- 所以,数据越接近正序,直接插入排序的算法性能越好。
- 稳定性: 不需要改变相等数值元素的位置,所以它是稳定的算法。
图解
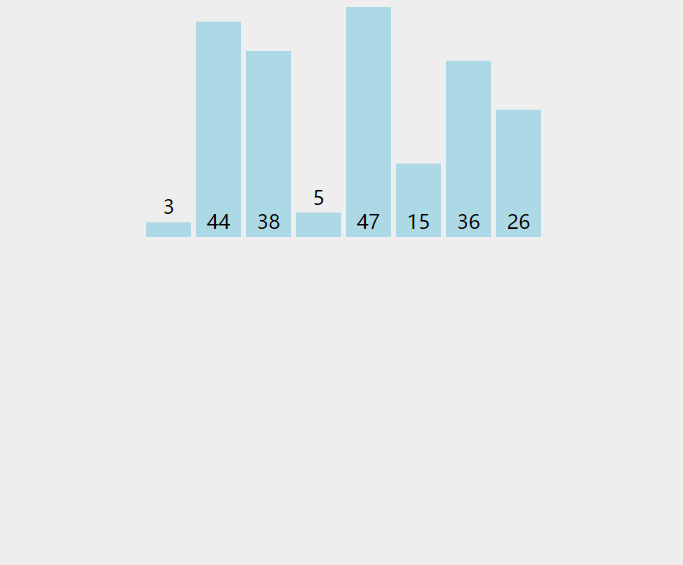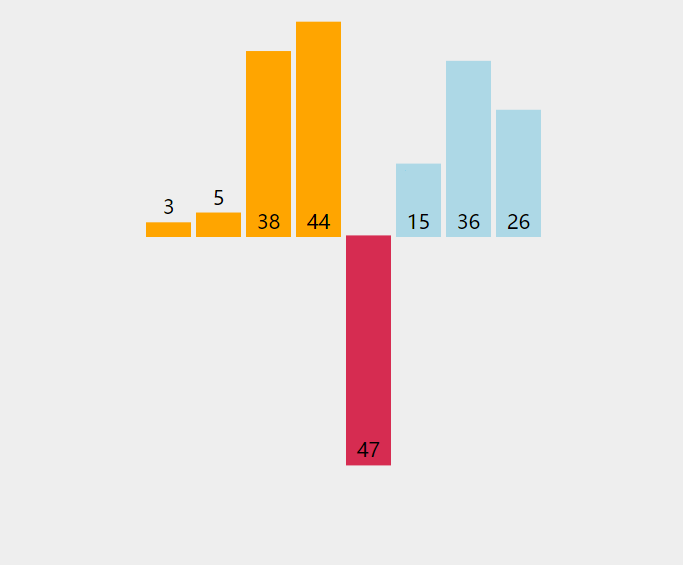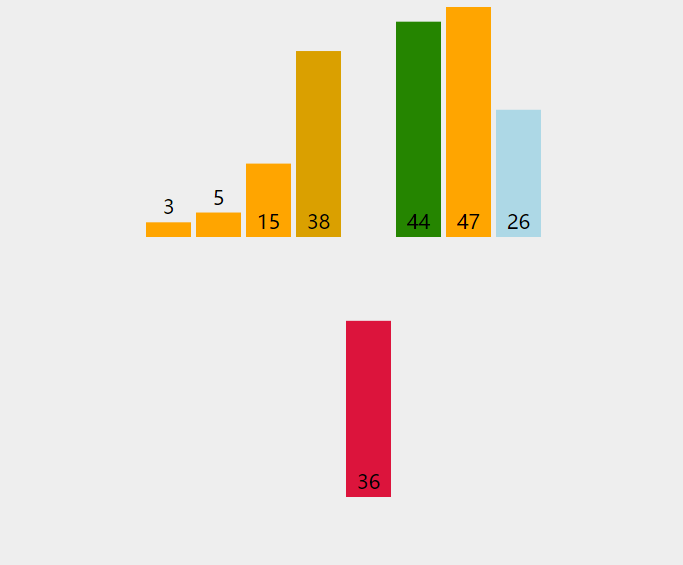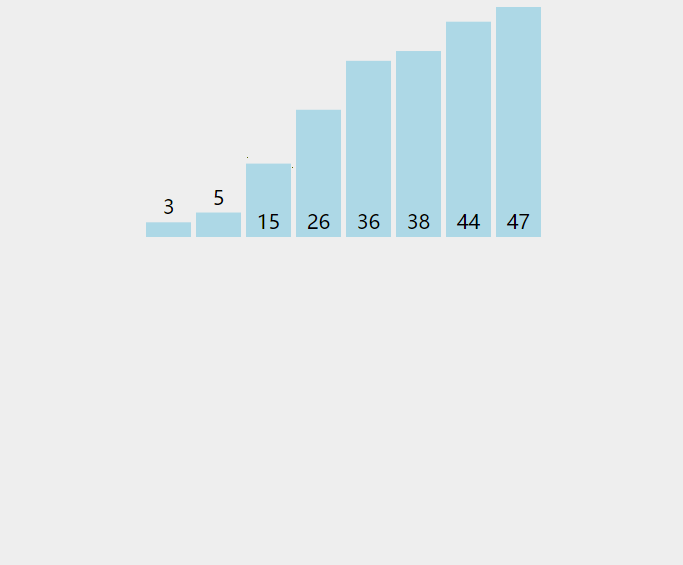
代码实现
1 | def insert_sort(li): |
